二次方程式の解き方は3パターン存在しています(後ほど詳しく解説します)
しかし、高校生の中にはその3パターンのうちどれを使えば良いのか?の見分け方がわからないという人もいるのではないでしょうか?
そこで今回は、早稲田大学教育学部数学科を卒業した筆者が二次方程式の解き方3パターンについて解説した後、解き方の見分け方についても解説します。
数学が苦手な人でも二次方程式が解けるようにわかりやすく解説しているので、ぜひ最後までご覧ください。
※二次方程式とは何かについて解説した記事もご用意しているので、ぜひ参考にしてください。
二次方程式の解き方その1:因数分解
二次方程式の解き方1つ目は因数分解を利用することです。
例として以下の二次方程式を解いてみましょう。
【例題】
二次方程式x2-15x+36=0を解きなさい。
【解答&解説】
x2-15x+36を因数分解すると(x-3)(x-12)となりますね。
※因数分解のやり方について解説した記事もご用意しているので、ぜひ参考にしてください。
つまり、(x-3)(x-12)=0となるわけです。
2つの数を掛け算して0になるので、x=3=0またはx-12=0となります。
したがってx=3、12・・・(答)となるわけです。
以上のように、因数分解を利用して二次方程式を解くのは基本中の基本となります。因数分解についてはたすき掛けを必ずできるようにしておきましょう。
因数分解を使って二次方程式を解く方法についてもっと詳しく解説した記事もご用意しているので、ぜひ参考にしてください。
二次方程式の解き方その2:平方完成
二次方程式の解き方2つ目は平方完成を利用することです。
こちらも例題を使って解説していきます。
【例題】
二次方程式x2+12x-8=0を解きなさい。
【解答&解説】
x2+12x-8を平方完成することを考えます。
平方完成とは二次式を(x-p)2+qに変形させることでした。
x2+12x-8のxの係数が12であることに注目して平方完成すると、(x+6)2-44となりますね。
※平方完成のやり方について解説した記事もご用意しているので、ぜひ合わせてご覧ください。
つまり、(x+6)2-44=0となるわけです。
44を右辺に移行して、(x+6)2=44となるので、x+6=±2√11となりますね。
※x+6=±2√11になる理由がわからない人は平方根とは何かについて解説した記事をご覧ください。
したがってx=-6±2√11・・・(答)となります。
平方完成は二次方程式を解くだけでなく、二次関数の頂点の座標を求めたりするときにも利用します。
大学入試や共通テストでもかなり頻出なので、必ずできるようにしておきましょう。
平方完成(平方根)を使って二次関数を解く方法について詳しく解説した記事もご用意しているので、ぜひ参考にしてください。
二次方程式の解き方その3:解の公式
二次方程式の解き方3つ目は解の公式を使うパターンです。
解の公式を簡単におさらいしておくと、二次方程式ax2+bx+c=0の解はx=-b±√(b2-4ac) / 2aとなるのでした。
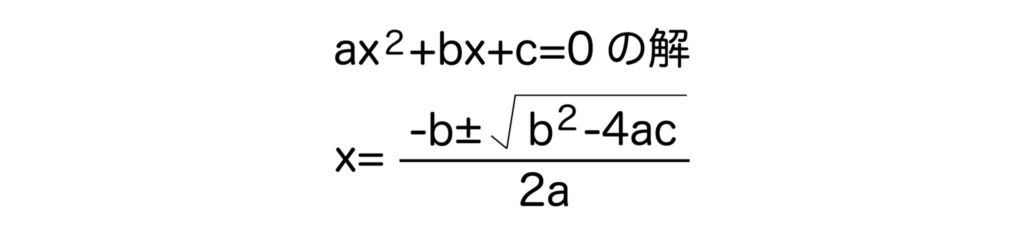
※詳しくは二次方程式の解の公式について解説した記事をご覧ください。
すべての二次方程式は解の公式を使えば必ず解くことができます。つまり、与えられた二次方程式が因数分解できなさそうで、平方完成をするのもめんどくさそうな場合は解の公式を使えば必ず解けます。
では、例題です。
【例題】
二次方程式x2+√5x+1=0を解きなさい。
【解答&解説】
解の公式よりa=1、b=√5、c=1となるので
x = -√5±√5-4 / 2 = -√5±1 / 2・・・(答)となります。
解の公式を使えば二次方程式は必ず解けるということをぜひ頭に入れておいてください。
二次方程式の解き方の見分け方
以上で二次方程式の解き方を3つ(因数分解・平方完成・解の公式)ご紹介してきましたが、二次方程式が与えられたとき、3つのうちどれを使って解けばいいのか?の見分け方がわからないという相談をよく受けます。
結論としては、まずは当てられた二次方程式が因数分解できないか?を考えましょう。
因数分解を利用して二次方程式を解くのが最も簡単な方法です。たすき掛けができないか?をぜひ考えてみてください。
そして、因数分解できない場合は解の公式を使うことをおすすめします。
先ほども解説した通り、解の公式を使えば二次方程式は必ず解けます。解の公式は最強の手段だと思っておきましょう。
解の公式を使う際には、ax2+bx+c0=0のxの係数に注目してください。xの係数が偶数の場合はx=-b’±√(b’2-ac) / aとなるので、少し計算が楽になります(b=2b’とする)
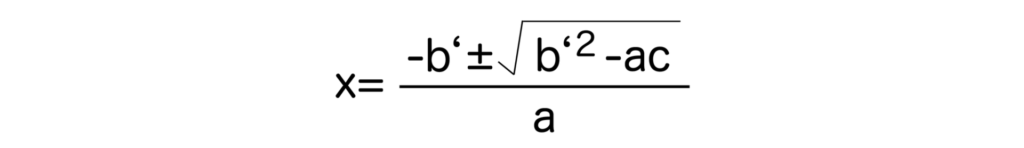
二次方程式を解く練習問題
最後に、二次方程式を5問解いてみましょう。
因数分解、平方完成、解の公式どれを使ってもOKです。一番簡単に解けそうな方法を選んでみてください。
【練習問題】
以下の二次方程式を解きなさい。
(1)2x2+3x-20=0
(2)5x2-14x-3=0
(3)x2+5x+5=0
(4)x2+2√2x-3=0
(5)1/3x2-5/2x+1=0
【解答&解説】
(1)2x2+3x-20を因数分解すると(2x-5)(x+4)になるので、x=5/2、-4・・・(答)となります。
(2)5x2-14x-3を因数分解すると(5x+1)(x-3)となるので、x=-1/5、3・・・(答)となります。
(3)x2+5x+5は因数分解できそうにないので解の公式を使いましょう。
x=-5±√52-4×1×5/2×1=(-5±√5)/2・・・(答)となります。
(4)解の公式より、x=-√2±√2-(-3)=-√2±√5・・・(答)となります。
(5)両辺に6をかけて分数を消去しましょう。すると、
2x2-15x+6=0となるので、解の公式より、
x=15±√152-4×2×6/2×2=15±√177/4・・・(答)となります。
二次方程式に分数が含まれている場合の解き方について詳しく解説した記事もありますので、ぜひ参考にしてください。
いかがでしたでしょうか?
今回は二次方程式の解き方3パターンをご紹介していきました。解き方の見分け方としては因数分解→解の公式という順番をぜひ覚えておきましょう。


